8.třída

Geogebra v akci podruhé: Thaletova kružnice

Thaletova věta říká:

Pro libovolný trojúhelník ABC platí:
Jestliže je ABC pravoúhlý trojúhelník s přeponou AB, leží vrchol C na kružnici k s průměrem AB,
a  jestliže vrchol C leží na kružnici k s průměrem AB, je trojúhelník ABC pravoúhlý trojúhelník s přeponou AB.

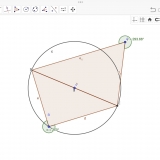
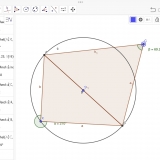
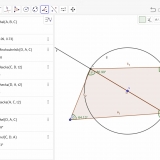
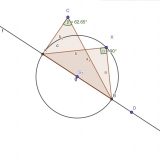
Jak pomocí geogebry dokázat její platnost? Sestrojili jsme úsečku AB a následně její střed. Z bodu S kružnici o poloměru SA. Na kružnici jsme zvolili bod C. Pak jsme setrojili trojúhelník ABC. Zvýraznili jsme úhel ACB a zobrazili jeho velikost. Pokud jsme pohybovali bodem C po kružnici velikost úhlu byla pořád 90°. Pro porovnání jsme ještě zvolili bod D, který neleží na kružnicii a zjistili jsme, že pro něj Thaletova věta neplatí. Velikost úhlu byla v případě, kdy ležel vně kružnice menší než 90°. Když ležel uvnitř kružnice, větší než 90°.

I když tato úloha byla pro začátečníky s geogebrou náročnější, osmáci se s ní zvládli dobře popasovat.

Mgr. Vladislava Hurajová